Mission
The Geo-Mathematical Imaging Group (GMIG) at Purdue University is a unique, industry and government (NSF, DOE) funded, multidisciplinary and interinstitutional graduate educational and research program in inverse problems and subsurface energy, with the broader purpose of advancing the understanding of our planet's interior and developing fundamentally new technologies, with leading faculty from Mathematics, Computer Science, Physics, and Earth, Atmospheric and Planetary Sciences.
The program's mission is to meet the complex challenges of modern day prospect evaluation and general geological study of Earth's interior by expanding the boundaries of knowledge of seismic imaging and inverse problems and by controlling and reducing computational costs.
Building on the combined expertise of GMIG's research team, the goals are the development of new geophysical probes, accounting for realistic physics and geology, to map and characterize multiscale structures and variations in rock properties, and connect them to the relevant geological, geodynamical and fluid flow processes.
GMIG's research broadly focuses on
- a fundamentally new perspective on local nonlinear (iterative) full waveform inversion, based on discovering conditional well-posedness and Lipschitz stability estimates (having pioneered convergence results), iterative regularization, multi-level methods and a nonlinear inverse problem analogue of compressed sensing leading to HIERARCHICAL SUBSURFACE ARCHITECTURES
- exploiting the analysis of inverse problems (pertaining to uniqueness with partial or finite data), we seek stability estimates driven parametrizations, estimates for stability constants driven schemes, iterative (multi-level, sparsity)regularization and approximation
- opening the way for direct nonlinear methods both in frequency and time domains under different conditions for global (approximate) reconstruction
- fast algorithms, massively parallel and extreme-scale computing based on new developments in numerical linear algebra introducing the use of HSS STRUCTURED MATRICES, compression and randomization
- novel high-dimensional signal representations in MULTISCALE FEATURE SPACES, manifold learning and spectral graph techniques for dimensionality reduction, segmentation, and interactive visual analysis, classification of seismic phases, hierarchical grammar for seismograms, and automatic geometric reconstruction of 4D wave fronts and wavefield recovery
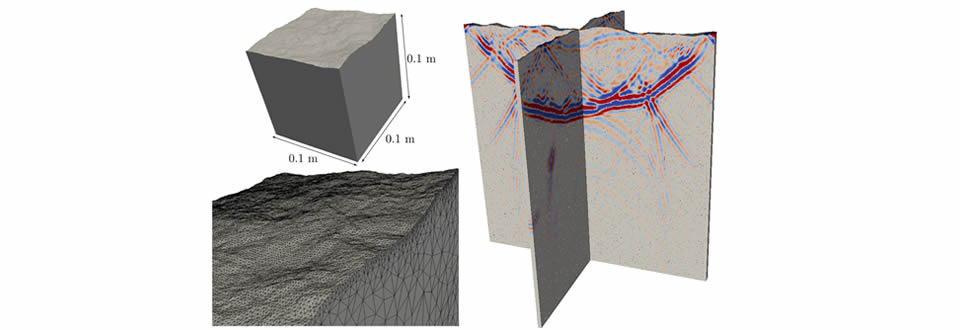
- wave interaction with systems of fractures in porous media, definition of critical geometric scales for a universal scaling relationship among the hydraulic, mechanical and seismic properties of fracture networks, resolving competing attenuation mechanisms from microstructures versus intrinsic anisotropy, mapping into a DIGITAL FRAMEWORK for (numerical) DYNAMIC UPSCALING, and micro-fluidic scale experiments to study the dynamic control and redistribution of immiscible fluids and colloids in fractured porous media
Geophysical prospecting is faced with the unraveling of geological structures, processes and rock properties in all their (multi-scale) complexity with ever increasing data volumes. Synergy between the lead researchers of our program leads to new methodologies that address these challenges pertaining to
- data structures, reduction and acquisition (based on data operators)
- exploiting and mitigating physical noise (coda and clutter)
- hierarchical subsurface representations derived from common unstructured meshes, with deformation and local multiscale refinement
- multi-scale probabilistic approaches, consistent with conditional well-posedness, below a data-determined resolution
We accomplish our goals through collaborative scientific activities in
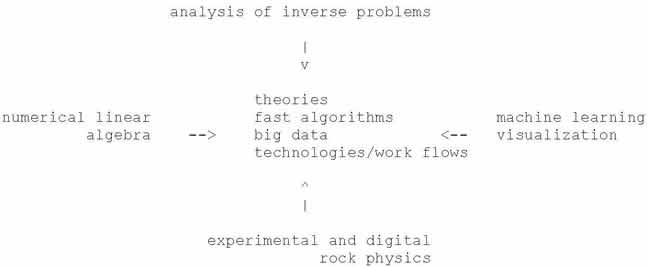
with a core in mathematics.
In the program, exploration seismology meets (teleseismic) global seismology, integrating and assimilating passive source (earthquake, aftershock, microseismic), ambient-noise source with active source data. Studies of diffuse electromagnetic inverse problems and hybrid inverse problems based on nonlinear coupled physics are part of GMIG's research portefolio.
Since its inception in 2007, GMIG has been widely recognized for developing analysis and algorithms pertaining to
- multi-scale physics of waves
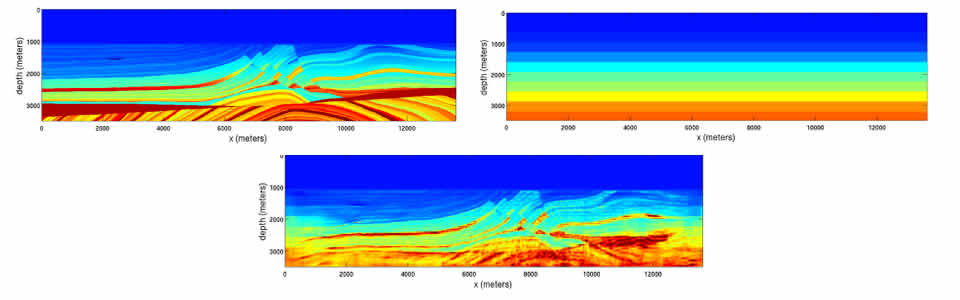
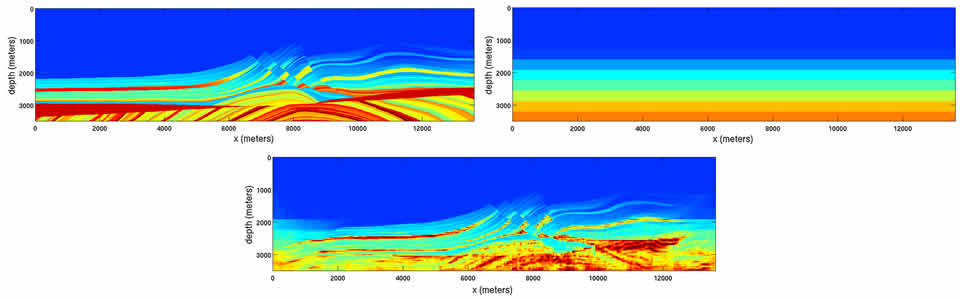
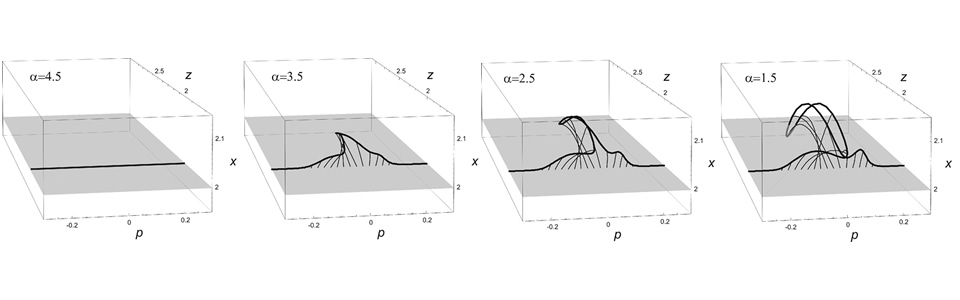
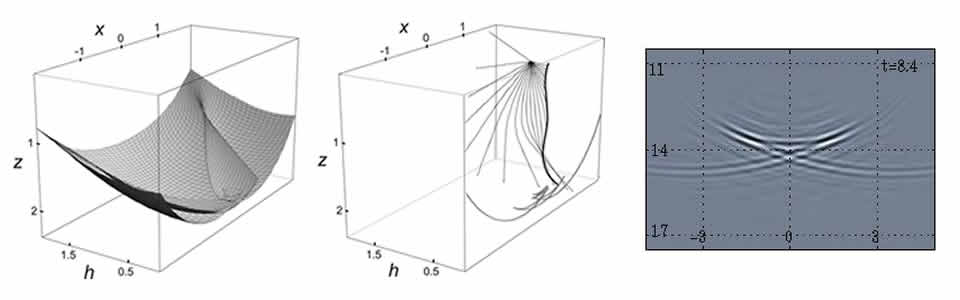
- In building a detailed understanding of the propagation and scattering of waves, that is, their interaction with complex media and boundaries, we have followed a hierarchical description of medium variations or coefficients, starting with a smooth component, a C^{1,1} component, general interfaces with regularity constraints, and a class of random fluctuations. The underlying analysis revealed a constructive description of ray-wave duality.
- Following the multi-scale analysis, we developed fast algorithms for propagation (one-way in pseudodepth and in time), imaging and inverse scattering (partial reconstruction) based on the dyadic parabolic decomposition of phase space and sparsity based regularization.
- data compression and operator probing, sparse representations
- Wavepackets and curvelets, for a given scale and orientation, are positioned via translation on a lattice. Naturally the points in the lattice have no knowledge of the waves in the data. We developed a nonlinear technique where the points become a function of the data to be decomposed, thus departing from the use of frames, and obtain optimal compression. This technique makes use of block Hankel operators and so-called AAK theory.
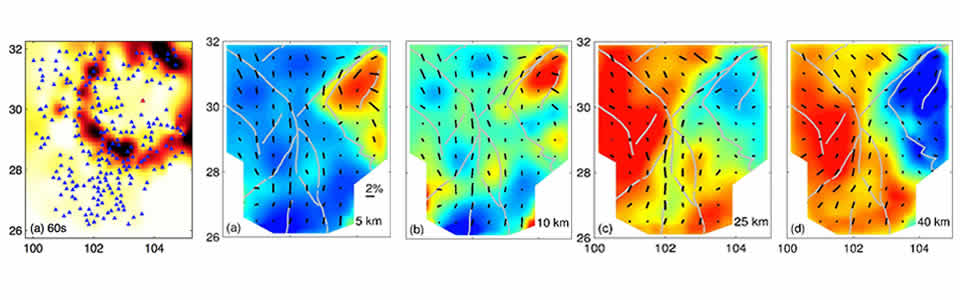
- For the seismic inverse problem, in our procedures, the data are the hyperbolic Neumann-to-Dirichlet map or the time-harmonic (elliptic) Dirichlet-to-Neumann map (or single-layer potential operator). Analyzing the properties of these operators, their matrix representations and (rank) structures, provided insight in optimal probing these. Probing corresponds with simultaneous sources acquisition.
- caustics, imaging and annihilator-based velocity inversion (~WEMVA)
- We developed a comprehensive understanding and mitigation of artifacts in acoustic and anisotropic elastic wave imaging in the presence of low-velocity zones and complex structures, casting the reverse-time continuation (RTM) and downward-continuation based imaging (via extensions we pioneered before) in an evolution-equation framework and developing inverse scattering transforms (for discontinuities) that also provide preconditioners for FWI.
- The evolution-equation framework provides a new approach to and understanding of recovery (resolution) of annihilator-based velocity inversion (~WEMVA) exploiting the mentioned ray-wave duality and including a gradient flow for velocity continuation.
- We enriched the imaging and ~WEMVA with certain classes of multiple scattered waves, and integrated (exploration) reflection seismic with teleseismic imaging and ~WEMVA naturally enhancing (multiparameter) illumination and resolution.
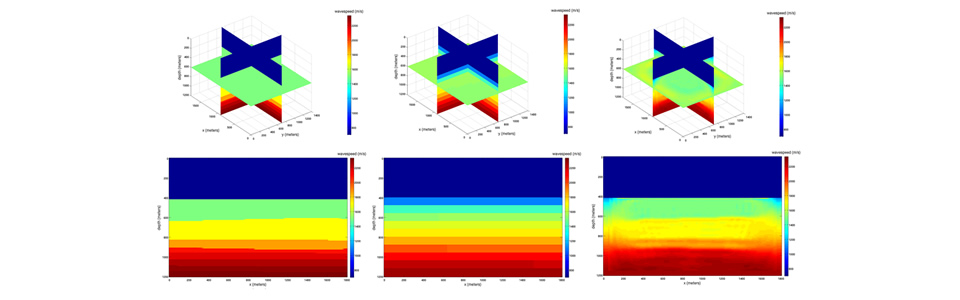
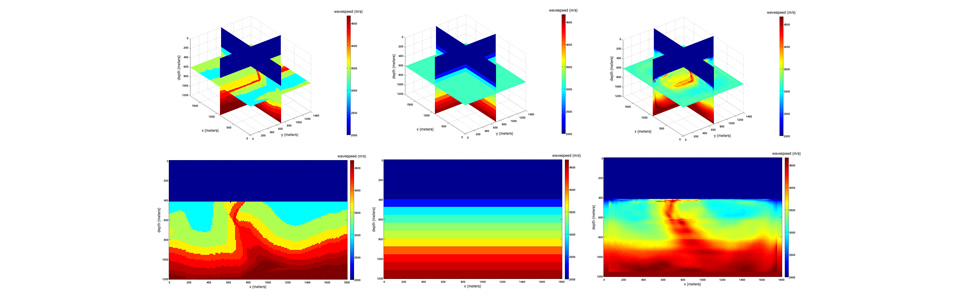
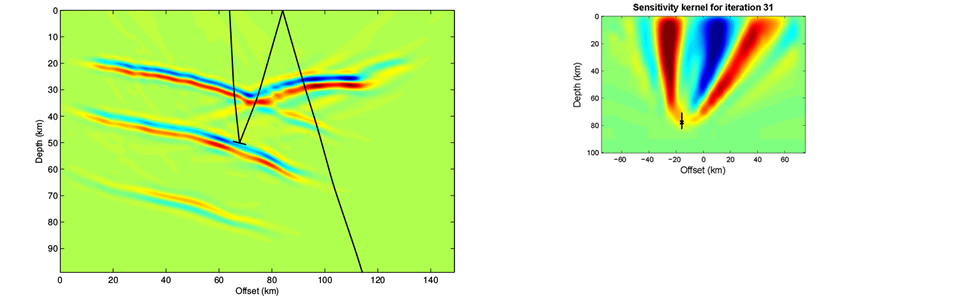
- local nonlinear iterative methods for inversion (FWI)
- fast algorithms, massively parallel computing, modelling
- We introduced massively parallel structured direct solvers using Hierarchically Semi-Separable matrices, transforming the way time-harmonic waves are computed, thereby approaching linear complexity. We exploit the fact that data are acquired with limited accuracy and use techniques to control finite accuracy computation.
- We developed a novel DG method approach to simulate acousto-elastic waves in time.
- Both of these algorithms play a critical role in the development of our iterative inverse (fast Newton-type) methods.
- rock physics
- Our research spans a range of topics related to elastic wave propagation in fractured porous media, interaction between fluids and solids, scale and size effects of material properties and multiphase flow.
- Scaling relationships for fractured media: We determined a flow-stiffness scaling relationship that provides a link between fluid flow and the seismic response of a fracture.
- We derived theoretically and confirmed experimentally the existence of a new coupled-wedge wave that propagates along surface fractures. These waves provide the first insight on the effect of intersections on elastic wave propagation.
- The presence of fractures can mask the intrinsic anisotropy of a material. We demonstrated experimentally that discrete and guided wave modes help unravel competing anisotropy from icrostructure versus intrinsic anisotropy.
- We have shown experimentally that swarms of micron-scale particles exhibit enhanced speed for an optimal range of fracture apertures enabling coherent transport of millions of particles.
- Immiscible fluid displacement: We have found that pinned water films in microfluidic channels act as elastic tether increasing the pressures needed to achieve full or partial saturation.
The innovation of GMIG's research can be substantiated by the rankings of the mathematics, physics and geophysics journals in which we publish extensively. Moreover, our work has also found application [data] in studying Earth's deep interior, results of which have been published in Science and PNAS. Major software packages developed by GMIG include
- wave packets: 3D transform pair and wave propagation allowing the formation of caustics
- fast RTM-type imaging and angle transform using the dyadic parabolic decomposition of phase
- DG method for modelling acousto-elastic waves in anisotropic solid-fluid media in 3D
- massively parallel direct structured solver for time-harmonic scalar waves in 3D (geometric approach, structured mesh or grid)
- massively parallel direct structured solver for time-harmonic elastic waves in 3D (geometric approach, structured mesh or grid)
- 3D scalar multi-level (multi-frequency, multi-scale), hierarchical compressed FWI
- 3D isotropic elastic multi-level (multi-frequency, multi-scale), hierarchical compressed FWI
Latest Publications
Particle swarms in smooth-walled fractures
, E.R. Boomsma and L.J. Pyrak-Nolte,
2014 View
Interface waves along fractures in anisotropic media
, S. Shao and L.J. Pyrak-Nolte,
2013 View
Coupled wedge waves
, B.C. Abell and L.J. Pyrak-Nolte,
2013 View