Research Summary
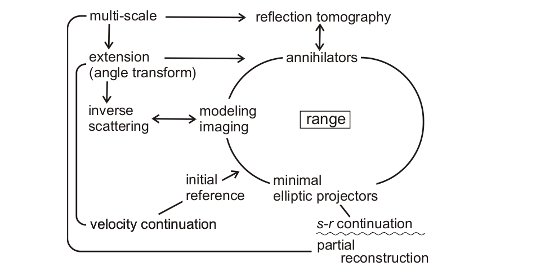
GMIG faculty and their collaborators pioneered the notions of (i) extensions and annihilators in imaging and inverse scattering based on the single scattering approximation, (ii) partial reconstruction using curvelets, and (iii) ray-wave duality using multi-scale analysis. The extensions lead to microlocally invertible operators critical in the process of velocity inversion using annihilators in the presence of caustics, while they also lead to Fourier integral operators associated with canonical graphs, which are amenable to compression and fast algorithms again using multi-scale techniques and prolate sphedroidal wave functions.
Key results in 2013-2014 include the development of a nonuniform sampling theory for multi-sensor data, as well as a nonlinear diffusion in the acquisition surface approach via a functional in full waveform inversion of finite multi-sensor data; the analysis of, and development of an algorithm for, the time-dependent inverse source problem, with applications to microseismic monitoring and the reconstruction of ruptures; the application of boundary control theory to generating virtual interior point sources or diffractors from the Neumann-to-Dirichlet map (that is, surface data) which is connected to nonlinear velocity inversion; multi-parameter conditional Lipschitz stability estimates controlling convergence of elastic full waveform inversion, that is, the inverse boundary value problem for time-harmonic elastic waves, in isotropic media with the Neumann-to-Dirichlet map representing vibroseis data; the semi-classical analysis of surface waves and surface-wave inversion for the reconstruction of the (anisotropic) shallow subsurface; and the analysis of the diffuse electromagnetic inverse problem, in particular, obtaining the Lipschitz stable recovery of resistivity and permittivity via electroseismic conversion; the development of a new, highly efficient parallel randomized HSS algorithm for dense matrix computations including the ones in the direct structured solver for (scalar and elastic) time-harmonic waves discretized on unstructured (tetrahedral) meshes.
Moreover, we obtained a sharp upper bound of the stability constant in the case of the inverse boundary value problem for the Helmholtz equation, in terms of the properties of the underlying mesh and frequency. Here, we associate a domain partitioning with an unstructured tetrahedral mesh. The upper bound plays a key role in our multi-level (multi-scale, multi-frequency) approach to full waveform inversion. We are continuing to make significant progress in developing the time-domain (hyperbolic) counterparts of our techniques in time-harmonic full waveform inversion.
We have initiated a new (multi-year) project on learning theory and classification, visualization and big data in collaboration with S. Mallat.



